令和6年春期試験問題 午前Ⅱ 問3
問3解説へ
1時間当たりの平均通話回数が60で,平均保留時間は120秒である。呼損率を0.1にしたいとき,必要な回線数は最低幾らか。ここで,表中の数値は加わる呼量(アーラン)を表す。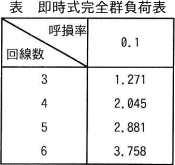

- 3
- 4
- 5
- 6
正解 イ問題へ
分野 :テクノロジ系
中分類:ネットワーク
小分類:ネットワーク方式
中分類:ネットワーク
小分類:ネットワーク方式
広告
解説
アーランは、単位時間当たりのトラフィック量を表す単位です。1アーランは、単位時間に1本の回線を100%利用したときのトラフィック量を表します。「トラフィック量が1回線の能力の何倍であるかを示すもの」と考えるとイメージしやすいと思います。呼損率とは、回線の空きがなく接続できなかった割合を示します。
設問の条件を整理して、呼量を計算していきます。
120秒×60回=7,200秒
1時間は3,600秒なので、このときの呼量は次のように計算します。
7,200秒÷3,600秒=2アーラン
この呼量を「即時式完全群負荷表(アーランB式)」に当てはめて必要な回線数を求めます。呼損率を0.1に設定した場合、呼量2アーラン以上を満たすには少なくとも4回線が必要になるとわかります。したがって「イ」が正解です。
設問の条件を整理して、呼量を計算していきます。
- 1時間当たりの平均通話回数が60回
- 平均保留時間(回線使用時間)は120秒
120秒×60回=7,200秒
1時間は3,600秒なので、このときの呼量は次のように計算します。
7,200秒÷3,600秒=2アーラン
この呼量を「即時式完全群負荷表(アーランB式)」に当てはめて必要な回線数を求めます。呼損率を0.1に設定した場合、呼量2アーラン以上を満たすには少なくとも4回線が必要になるとわかります。したがって「イ」が正解です。
広告